FATORES QUE INFLUENCIAM O CALOR DAS REAÇÕES OU ENTALPIA
A entalpia de uma ocorrência, que representa a variação da energia térmica quando uma ocorrência ocorre à pressão constante, é influenciada por diversos fatores. Aqui estão alguns dos principais:
- Estado físico dos reagentes e produtos : A fase (sólida, líquida ou gasosa) em que os reagentes e produtos se encontram pode afetar a entalpia. Por exemplo, a vaporização e a fusão exigem energia, enquanto a condensação e a solidificação liberam energia.

- Energia de ligação : A energia necessária para romper ou formar ligações químicas influencia diretamente a entalpia de ocorrência. Reações que exigem a quebra de ligações fortes geralmente têm entalpias mais elevadas, enquanto a formação de ligações fortes geralmente libera mais energia.
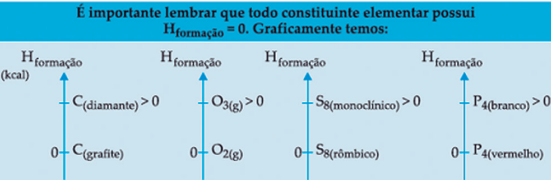
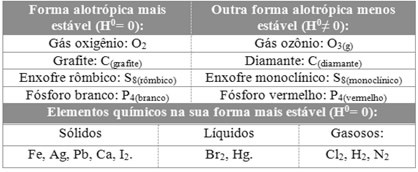
- Estado padrão dos reagentes e produtos : Cada substância tem uma entalpia padrão, que é uma entalpia de formação sob condições padrão (25°C e 1 atm). As entalpias de formação dos reagentes e produtos determinam o valor da entalpia de fato.
- Temperatura : A entalpia de uma ocorrência pode variar de acordo com a temperatura. Isso ocorre porque a capacidade calorífica dos reagentes e produtos, que muda com a temperatura, influencia a quantidade de energia trocada com o ambiente.
- Pressão : Em reações envolvendo gases, a pressão influencia a entalpia de ocorrência, especialmente em sistemas onde há variação de número de mols gasosos entre reagentes e produtos (devido ao trabalho de expansão ou variação dos gases).
- Natureza da ocorrência (exotérmica ou endotérmica) : Reações exotérmicas liberam calor (entalpia negativa), enquanto reações endotérmicas absorvem calor (entalpia positiva). A tendência de liberar ou absorver calor depende da espessura química dos reagentes e da estabilidade dos produtos.
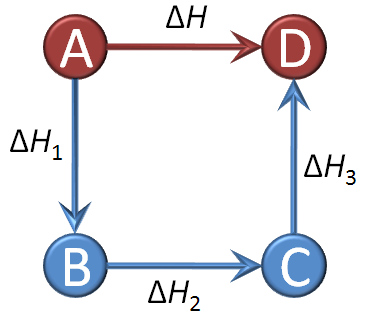
LEI DE HESS
A Lei de Hess é um princípio fundamental da termodinâmica que afirma que a entalpia total de uma ocorrência química depende apenas dos estados inicial e final, e não do caminho percorrido para realizar a ocorrência. Em outras palavras, a variação de entalpia de uma ocorrência é a mesma, independentemente de ser realizada em uma ou em várias etapas.
Fundamentos da Lei de Hess
A Lei de Hess é baseada na propriedade de que a entalpia é uma função de estado . Isso significa que a variação da entalpia de um sistema depende apenas das condições iniciais e finais e é independente do caminho ou dos passos intermediários da ocorrência. Se uma ocorrência pode ser dividida em várias etapas, a variação total da entalpia é a soma das variações da entalpia de cada etapa.
A variação da entalpia pode ser calculada subtraindo a entalpia inicial (antes da reação) da entalpia final (depois da reação):
ΔH = Hf – Hi
Outra forma de calcular é através da soma das entalpias em cada uma das reações intermediárias. Independente do número e tipo das reações.
ΔH = ΔH1 + ΔH2
Uma vez que esse cálculo considera apenas os valores inicial e final, conclui-se que a energia intermédia não influencia no resultado da sua variação.( https://www.todamateria.com.br)
Exemplo de resolução usando Lei de Hess
1. (Fuvest-SP) Com base nas variações de entalpia associadas às reações a seguir:
N2(g) + 2 O2(g) → 2 NO2(g) ∆H1 = +67,6 kJ
N2(g) + 2 O2(g) → N2O4(g) ∆H2 = +9,6 kJ
Pode-se prever que a variação de entalpia associada à reação de dimerização do NO2 será igual a:
2 NO2(g) → 1 N2O4(g)
a) –58,0 kJ b) +58,0 kJ c) –77,2 kJ d) +77,2 kJ e) +648 kJ
Resolução:
Passo 1: Inverter a primeira equação. Isso porque o NO2(g) precisa passar para o lado dos reagentes, conforme a equação global. Lembre-se que ao inverter a reação o ∆H1 também inverte o sinal, passando para negativo.
A segunda equação é conservada.
2 NO2(g) → N2(g) + 2 O2(g) ∆H1 = – 67,6 kJ
N2(g) + 2 O2(g) → N2O4(g) ∆H2 = +9,6 kJ
Passo 2: Observe que N2(g) aparece nos produtos e reagentes e o mesmo acontece com 2 mol de O2(g).
2 NO2(g) → N2(g)+ 2 O2(g)∆H1 = – 67,6 kJ
N2(g) + 2 O2(g) → N2O4(g) ∆H2 = +9,6 kJ
Assim, eles podem ser cancelados resultando na seguinte equação:
2 NO2(g) → N2O4(g).
Passo 3: Você pode observar que chegamos a equação global. Agora devemos somar as equações.
∆H = ∆H1 + ∆H2
∆H = – 67,6 kJ + 9,6 kJ
∆H = – 58 kJ ⇒ Alternativa A
Pelo valor negativo de ∆H também sabemos que trata-se de uma reação exotérmica, com liberação de calor.( https://www.todamateria.com.br/)
Exercício:
Um passo do processo de produção de ferro metálico, Fe(s), é a redução do óxido ferroso (FeO) com monóxido de carbono (CO).
FeO(s) + CO(g) → Fe(s) + CO2(g) ∆H = x
Utilizando as equações termoquímicas abaixo e baseando-se na Lei de Hess, assinale a alternativa que indique o valor mais próximo de “x”:
Fe2O3(s) + 3 CO(g) → 2 Fe(s) + 3 CO2(g) ∆H = -25 kJ
3 FeO(s) + CO2(g) → Fe3O4(s) + CO(g) ∆H = -36 kJ
2 Fe3O4(s) + CO2(g) → 3 Fe2O3(s) + CO(g) ∆H = +47 kJ
a) -17 kJ.
b) +14 kJ.
c) -100 kJ.
d) -36 kJ.
e) +50 kJ.
RESOLUÇÃO
O valor que queremos descobrir é o da variação da entalpia da reação:
FeO(s) + CO(g) → Fe(s) + CO2(g) ∆H = x
Segundo a lei de Hess, a variação da entalpia de uma reação depende somente da entalpia do estado final e inicial, independentemente se a reação ocorreu em uma única etapa ou em mais. Por isso, podemos somar as três reações e descobrir o valor do “x”. Mas observe que é preciso multiplicar a primeira equação por 3 e a segunda por 2:
3 Fe2O3(s) + 9 CO(g) → 6 Fe(s) + 9 CO2(g) ∆H = -75 kJ
6 FeO(s) + 2 CO2(g) → 2 Fe3O4(s) + 2 CO(g) ∆H = -72 kJ
2 Fe3O4(s) + CO2(g) → 3 Fe2O3(s) + CO(g) ∆H = +47 kJ
6 FeO(s) + 6 CO(g) → 6 Fe(s) + 6 CO2(g) ∆H = -100 kJ
Dividindo a equação inteira por 6, inclusive o valor de ∆H, temos o seguinte valor aproximado:
FeO(s) + CO(g) → Fe(s) + CO2(g) ∆H = -17 kJ
https://exercicios.brasilescola.uol.com.br/